검색결과 리스트
분류 전체보기에 해당되는 글 86건
- 2014.12.11 정현파 신호
- 2014.12.11 주파수(frequency)란?
- 2014.12.11 Sampling Theorem
- 2014.12.11 A/D conversion (Analog to Digital) 과정
- 2014.12.10 신호(signal)란 무엇인가
- 2014.12.09 [C/C++] double 형 데이터에 분수 넣기
- 2014.12.04 서보모터(servo motor)와 스텝모터(step motor)의 차이
- 2014.12.04 케이블 배선 꼬는 이유..
- 2014.12.02 Fourier Transform (푸리에 변환)
- 2014.11.13 스페인 저가항공 부엘링(Vueling) 예약하기 (마드리드에서 바르셀로나)
글
정현파 신호
A : magnitude
'Research > Digital Signal Processing' 카테고리의 다른 글
| Sampling의 기본 개념 (0) | 2014.12.16 |
|---|---|
| 주파수(frequency)란? (0) | 2014.12.11 |
| Sampling Theorem (0) | 2014.12.11 |
| A/D conversion (Analog to Digital) 과정 (0) | 2014.12.11 |
| 신호(signal)란 무엇인가 (0) | 2014.12.10 |
글
주파수(frequency)란?
1. 주파수의 협의적 의미
2. 주파수의 광의적 의미
Fourier 표현식에 따른 시간 변수 t의 또 다른 표현식
(신호를 표현하기 위한 또 다른 독립 변수 정도로...)
frequency에 대한 정의는 time에 대한 정의만큼 어렵다.
그러나 time과 Fourier 표현식 관계에 있따는 것은 알 수 있다.
'Research > Digital Signal Processing' 카테고리의 다른 글
| Sampling의 기본 개념 (0) | 2014.12.16 |
|---|---|
| 정현파 신호 (0) | 2014.12.11 |
| Sampling Theorem (0) | 2014.12.11 |
| A/D conversion (Analog to Digital) 과정 (0) | 2014.12.11 |
| 신호(signal)란 무엇인가 (0) | 2014.12.10 |
글
Sampling Theorem
샘플링 과정에서 충분한 조건을 만족하면 에러가 발생하지 않는다!?
The analog signal x_a(t) can be exactly reconstructed from its discrete time version x(n),
only if the sampling rate f_s is greater than or equal to the maximum frequency content of x_a(t)
(F_s >= F_max)
'Research > Digital Signal Processing' 카테고리의 다른 글
| Sampling의 기본 개념 (0) | 2014.12.16 |
|---|---|
| 정현파 신호 (0) | 2014.12.11 |
| 주파수(frequency)란? (0) | 2014.12.11 |
| A/D conversion (Analog to Digital) 과정 (0) | 2014.12.11 |
| 신호(signal)란 무엇인가 (0) | 2014.12.10 |
글
A/D conversion (Analog to Digital) 과정
A/D Conversion의 단계는 아래와 같다.
1. sampling
=> 독립변수를 쪼갠다. (보통은 시간)
쪼개는 간격을 sampling period라고 함
그 역수를 취하면 sampling rate, 즉 frequency가 됨
2. quantization
=> 종속변수를 쪼갠다.
쪼개는 간격을 quantization step size(resolution)라고 함
3. encoding
=> binary data가 어떤 의미를 갖는 지에 대한 약속
sampling과 quantization 모두 연속된 신호를 이산화 하는 과정이다.
(이 과정에서는 당연히 error가 발생할 수 있겠지?)
'Research > Digital Signal Processing' 카테고리의 다른 글
| Sampling의 기본 개념 (0) | 2014.12.16 |
|---|---|
| 정현파 신호 (0) | 2014.12.11 |
| 주파수(frequency)란? (0) | 2014.12.11 |
| Sampling Theorem (0) | 2014.12.11 |
| 신호(signal)란 무엇인가 (0) | 2014.12.10 |
글
신호(signal)란 무엇인가
시간, 공간 등의 독립변수에 의해서 변화하는 물리적인 양 (physical quantity)
독립변수를 x라하면 물리량은 f(x)로 표현할 수 있을 것이다.
즉, 신호는 수학적으로 표현이 가능하다는 것!
(그런데 얼마나 정확하게 표현이 가능할까에 대한 부분은 고민해 보아야 한다.)
신호를 수학적으로 표현하는 이유는 신호를 분석(혹은 규격화)하기 위함이고!
분석된 신호는 처리(processing) 된다. 그리고 신호를 합성하는 것까지.
신호의 분류
1) scalar? or vector?
ex) 콘덴서 마이크로폰 or 홈시어터
2) continuous time? or discrete time?
ex) 독립변수가 countable 하지 않음, countable 함 (예를 들면 실수와 정수)
3) continuous valued? or discrete valued?
ex) 종속변수 f가 연속적인 함수? or 불연속적인 함수?
4) deterministic? or random?
ex) 주어진 독립 변수에 대해 종속변수의 값을 정확히 알 수 있는지?
Digital signal은 discrete time이면서 discrete valued 의 성격을 갖는다.
보통 DSP에서 처리하는 신호는 엄밀하게 이야기하면
Digital signal이라기 보다는 descrete time signal이라고 보는 것이 맞다?
* 콘덴서 마이크로폰 (condenser microphone)
도전성을 가진 매우 얇은 막이 진동관과 고정 전극을 평행으로 배치하여 콘덴서를 만들고
음의 진동에 의한 용량의 변화로부터 전기적 출력을 얻는 것
'Research > Digital Signal Processing' 카테고리의 다른 글
| Sampling의 기본 개념 (0) | 2014.12.16 |
|---|---|
| 정현파 신호 (0) | 2014.12.11 |
| 주파수(frequency)란? (0) | 2014.12.11 |
| Sampling Theorem (0) | 2014.12.11 |
| A/D conversion (Analog to Digital) 과정 (0) | 2014.12.11 |
글
[C/C++] double 형 데이터에 분수 넣기
함수를 정의할 때, parameter로 double 형 데이터를 활용하게 되는 경우가 종종 있다.
그런데 이 때, 함수를 사용하는 쪽에서 double 형 데이터에 소수점 값을 넣게되는 경우가 있는데
소수점 값을 직접 입력하지 않고 분수로 값을 입력할 때 실수가 가장 많다.
예를 들면 아래와 같은 코드를 생각해 보자.
#include <stdio.h>
void test(double num)
{
printf("%lf \n", num);
}
int main()
{
test(0.001);
test(1/1000);
return 1;
}
이 때, 1/1000 을 넣으면 값은 0 이 나온다.
분수의 형태로 넣고 싶다면 1.0/1000.0 처럼 double 형으로 인식할 수 있도록 해 주어야 한다.
(혹은 casting을 해 주어도 괜찮다.)
'Skills > Programming' 카테고리의 다른 글
| C++ 반전 연산자~와 논리 연산자 !의 차이 (0) | 2014.12.16 |
|---|---|
| 공유 메모리를 이용한 IPC (0) | 2014.12.15 |
| MFC dialog에서 콘솔(console)로 디버깅하기 (0) | 2014.12.15 |
| 첫째 예외가 있습니다. 0xC0000005: 0x00000018 위치를 읽는 동안 액세스 위반이 발생했습니다. (0) | 2014.11.12 |
| 클래스 객체 생성 방법에 관하여.. (new 사용에 관하여) (0) | 2014.11.12 |
글
서보모터(servo motor)와 스텝모터(step motor)의 차이
* 이 글은 지속적으로 수정될 수 있음.
모션 제어기에서 스테핑 모터와 서보 모터의 위치연산의 방법은 다소 차이가 난다.
왜냐하면 스테핑 모터의 특성상 고속의 운전중에 공급되는 모션 제어 펄스의 주파수가 미세하게나마 진동을 하면 그 순간 바로 탈조 회전력을 잃어버리기 때문에 스텝 모터의 제어는 속도 제어에 기본은 둔 위치 제어를 구성하여야 한다.
그러나 서보 모터의 경우에는 고속의 펄스열에서 미세하게 주파수의 변동이 나타나더라도 모터의 회전 관성과 이를 서보 드라이버 내부의
제어 이득에 의하여 실제 모션의 출력에는 별다른 영향을 미치지 못하게 된다. 따라서 서보 모터의 경우
위치 제어는 Sampling Time에 의한 위치 제어방법을 구현하여 사용하고 있다.
이와 같은 이유로 스텝 모터의 회전중에 이송 편차를 보상하기가 어렵고, 따라서 Feedback 제어를 구현하기 어렵게 된다. 그리고 몇몇 제조사의 PLC 위치결정 Unit 혹은 서보 모터를 기준으로 개발된 모션 제어기는 사실상 스텝 모터를 고속에서 구동하기 어렵게 된다. 또한 스텝 모터 전용으로 개발되어진 모션 제어기는 비교적 낮은 주파수의 제어만을 할 수 있기 때문에 엔코더 분해능이 높은 서보 모터 및 드라이버를 구동하여 고속 운전을 하기가 어렵다.
그러므로 서보 드라이버 및 스테핑 드라이버와 동시에 구성이 가능하고 각각 독립적인 모션을 생성할 수 있는 제어기를 사용하면 다양한
모션의 구현이 가능하여진다.
스텝 모터를
제어하기 위하여 모션 제어기에 주어지는 파라미터를 <그림
8>에서 알 수 있으며 그 내용은 다음과 같다.
▶ 이송거리 S : 모터가 회전하여 이송할 전제 이송 펄스수를 설정
▶ 이송속도 V : 모터가 회전을 시작하여 도달하는 최고 속도
▶ 가속시간 T1 : 최고 속도까지 가속하여 도달하는 시간
▶ 감속시간 T3 : 최저 속도까지 감속하는 시간
▶ 속도 오프셋 Vo : 운전 시작과 끝에서 지정되는 속도
<그림1>스탭
모터 모션 제어의 일반적인 특성곡선
스텝 모터의 위치를 제어하기 위해서는 속도 제어를 하는 방법에 기준하여 제어를 한다고 하였는데, 그 이유는 스텝 모터 저속구간의 공진 주파수가 존재하기 때문이며 다른 한가지는 최고 이송속도 V의 설정값이 스텝 모터 Pull-Out Torque 가까이 운전이
되고 있을 때에 이송속도가 미소하게 진동하여도 바로 탈조가 발생되는 현상을 가지고 있기 때문이다.
그러므로 스텝 모터의 제어는 속도 오프셋 Vo를 운전 개시속도로 설정하고 속도곡선이 매우
부드럽도록 제어하여야 한다. 또한 가속시간 T1과 감속시간 T3 역시 운전에서 중요한 파라미터가 되며 지정된 시간을 참조하여 가속시간의 속도 순간 변화량을 계산하게 된다.
이러한 가감속시간은 스텝 모터의 운전영역을 Pull-Out 토크이내에서 운전하도록 설정하여야
한다.
<그림 1>과 같은 모션 제어곡선을 연산하기 위하여 모션 제어기는 마이크로 프로세서를
내장하고 있다. 이러한 마이크로 프로세서는 기준시간을 설정하고 단위시간이 경과하면 위치 제어를 위하여
단위시간당 변화하는 주파수를 설정하고, 이를 출력하여 제어하게 된다.
<그림 2>에 나타낸 것은 서보 모터를 이용한 위치 제어에 대한 특성곡선을 나타내었는데
여기서 스텝 모터의 경우 공진 주파수를 피하기 위한 속도 오프셋이 존재하지 않는다는 것을 볼 수 있다. 이것은
서보 모터의 특성이 제어이득의 설정에 따라 다소 차이가 발생하지만 저속구간에서 스텝 모터에서 볼 수 있는 공진현상 등은 나타나지 않으며 실제 운전에서
스텝 모터의 구동보다 부드러운 모션 제어를 구현할 수 있다.
<그림2>서보
모터 모션 제어의 일반적인 특성곡선
서보 모터의
위치 제어에서는 스텝 모터의 제어와는 달리 단위시간당 속도의 데이터를 연산하는 것이 아니고 단위시간당 위치의 편차량을 제어하게 된다. 이것은 마이크로 프로세서 내부에서 이송위치의 연산을 수행하고, 이를
다시 속도의 값으로 계산하여 출력하게 된다. 따라서 한번 더 연산을 수행하게 되는데 동시에 여러 개의
축을 제어하기 위하여 보다 성능이 좋은 프로세서를 요구하게 된다.
따라서 최근의 제어기들은 DSP(Digital Signal Processor) 혹은 RISC Processor 등을 채용하고 있다.
Ref. (or copied from)
[1] 모터 제어기와 모터 제어, 윤명균
[2] ..
'Research > Robotics' 카테고리의 다른 글
| why column vectors of rotation matrix is new axis ? (0) | 2015.03.11 |
|---|---|
| why use a homogeneous transform matrix? (0) | 2015.03.09 |
| difference between Euclidean and Cartesian (0) | 2015.03.04 |
| 케이블 배선 꼬는 이유.. (0) | 2014.12.04 |
| Robot Dynamics 초간단 정리 (0) | 2014.11.08 |
글
케이블 배선 꼬는 이유..
전기전자회로에 흐르는 신호는 크게 직류신호와 교류신호가 있는데...
(두가지가 한 도선에 섞여 같이 흐를 때도 있지만...)
서보선에 흐르는 신호는 일종의 펄스파로, 교류에 해당된다.
교류는 특성상 도선을 흐를때, 마치 전자석처럼, 미약하긴 하지만 자장을 발생 시키기도 하고, 도선 주위로 약한 전파(잡파)를 발생 시켜서 주위에 있는 다른 회로에 영향을 미치기도 한다.
특히, 모터는 잡파(artifact?)를 특히 많이 방출한다.
또, 전기가 흐를수 있는 모든 도선은 공중을 날아 다니는 전파(물론 잡파도...)를 흡수한다고 한다.. (Ex. 워커맨으로 FM라디오를 들을때 이어폰선이 안테나 역활을 하는 것)
그래서, 서보선은 모터의 잡파와 주변의 또다른 잡파들을 흡수함과 동시에 스스로도 미약한 잡파를 발생 시키기도 한다.
선에 전류가 흐를 때 발생하는 자기장은 전류가 변하는 것을 방해하여 고주파 특성이 나빠지게 한다.
선을 꼬면, 자기장이 서로 상쇄되게 만들어 결과적으로 자기장이 덜 생기게 되므로 고주파 특성이 좋아진다.
외부에서 발생한 자기장이 선에 기전력을 일으키는데, 선을 꼬아놓으면 그 기전력이 상쇄되어 노이즈에 민감하지 않게 된다.
'Research > Robotics' 카테고리의 다른 글
| why column vectors of rotation matrix is new axis ? (0) | 2015.03.11 |
|---|---|
| why use a homogeneous transform matrix? (0) | 2015.03.09 |
| difference between Euclidean and Cartesian (0) | 2015.03.04 |
| 서보모터(servo motor)와 스텝모터(step motor)의 차이 (0) | 2014.12.04 |
| Robot Dynamics 초간단 정리 (0) | 2014.11.08 |
글
Fourier Transform (푸리에 변환)
한 지점에서의 파동의 움직임을 계속 관측하면 주어진 각각의 시간에 파동량의 그래프를 그릴 수 있을 것이다. 이 그래프는 모든 시간 값에 대하여 대응되는 파동량을 가지고 있는 아날로그의 데이터일 것인데 이 신호를 컴퓨터를 통해서 읽으면 띄엄띄엄한 시간에 띄엄띄엄한 파동량의 디지털화 된 데이터로 될 것이다.
예를 들어 소리의 전기신호를 오실로스코프로 보면 음압이나 변위에 대한 연속적인 그래프가 화면에 바로 나타날 것이다. 이 신호를 푸리에 해석을 하여 주파수 성분을 추출하고자 한다면 앞에서 설명한 대로 여러번 적분을 행해야 할 것이다. 그러나 음압을 나타내는 전기신호는 보통 해석적인 함수가 아니므로 해석적으로 적분을 할 수 없게 되어 수치해석이 필요해 진다. 콘덴서나 코일 등의 소자를 구성해서 아날로그로의 푸리에 해석을 어느 정도는 해 낼 수 있지만 엄밀한 분석은 불가능하다.
컴퓨터를 이용한 신호분석
음파의 신호를 컴퓨터를 통해서 읽게 되면 수치해석을 컴퓨터의 연산능력으로 푸리에 해석을 할 수 있게 된다. 이 경우 컴퓨터는 신호의 변화에 대하여는 매우 짧은 시간간격이긴 하지만 어떤 유한한 간격으로 신호를 읽을 수밖에 없을 것이다. 측정의 시간 간격을 줄이면 줄일수록 원래의 아날로그 데이터에 근접하게 되겠지만 같은 시간분량에 대한 데이터 수는 시간간격에 반비례하여 늘어가게 되어 컴퓨터가 감당하지 못하게 된다. 한편 어떤 시간의 측정 값도 당연히 디지털화 된 신호일 수밖에 없다. 따라서 연속적인 모든 값을 표현하지 못하고 불연속적인 값들 중 하나로 나타내어지게 된다. 시간 축으로나 신호 축으로나 이렇게 띄엄띄엄하게 측정되는 것을 양자화되었다고 한다.
| graph |
 |
|
음악을 기록한 것 중 옛날의 LP 판은 음파의 변화를 연속적으로 기록해 둔, 일종의 아날로그형의 신호 기록으로 볼 수 있고, CD나 DAT 등은 음파를 디지털화 시켜 기록한 것으로 비교해 볼 수 있다. CD의 경우 1초에 4만번 이상으로 한 번에 16비트, 즉 6만 계단 이상으로 음을 기록해서 이를 재생하면 아날로그의 원형을 거의 완벽하게 재생해 낼 수 있게 된다. 아날로그 기록인 경우 신호가 정확하게 읽혀지지 않을 가능성이 있지만 값으로 기록된 디지털 기록은 언제나 정확하게 읽혀지게 되고 통신을 통해서도 정확하게 전달 시킬 수 있게 된다.
디지털화된 신호는 { 1.1, 1.2, 1.34, ... } 처럼 일종의 수열로서 시간 순서로 이루어져 있다면 시계열(time series)라고 한다. 이 데이터를 이제 컴퓨터에서 수치해석으로 적분하여 그 신호가 가지고 있는 각각의 주파수 성분, 즉 스펙트럼을 계산해 낼 수 있게 된다. 이에 관련된 기법을 DFT(discrete fourier transformation)라 하여 디지털 신호처리(DSP: digital signal processing) 기술의 핵심을 이루게 된다. 즉 음성인식이나 변조, 복원 등 여러 가지 기법이 DSP를 통해서 가능하게 되었다.
* 디지털 신호 처리
디지털 신호 처리(Digital signal processing, DSP)는 디지털화된 신호를 원하는 방향으로 정보 신호를 수정하거나 개선할 목적으로 알고리즘에 의해 수치적으로 처리하는 것을 말한다. 보통 아날로그 신호를 디지털화하는 과정에서 이산 신호가 되고 수치화 된다.
DSP의 일반적인 목적은 연속적인 실세계 아날로그 신호를 측정하고 걸러내고 압축하는 것이다. 첫 단계는 샘플링이라는 과정을 통해 신호를 아날로그에서 디지털 형태로 변환하는 것이고, 그 뒤 ADC를 이용하여 디지털화하여 아날로그 신호를 연속된 수로 바꾼다.
The goal of DSP is usually to measure, filter and/or compress continuous real-world analog signals. Usually, the first step is conversion of the signal from an analog to a digital form, by sampling and then digitizing it using an analog-to-digital converter (ADC), which turns the analog signal into a stream of discrete digital values. Often, however, the required output signal is also analog, which requires a digital-to-analog converter (DAC). Even if this process is more complex than analog processing and has a discrete value range, the application of computational power to signal processing allows for many advantages over analog processing in many applications, such as error detection and correction in transmission as well as data compression.[1]
FFT 해석
매우 빠르게 푸리에 분석을 수행한다.
분석해야 할 시계열의 데이터가
한편 데이터가
* Fourier Analysis
- Continuous-Time Fourier Series
- Continuous-Time Fourier Transform
- Discrete-Time Fourier Series
- Discrete-Time Fourier Transform
* Fourier Series
- A way to represent a wave-like function as the sum of simple sine waves.
More formally, it decomposes any periodic function or periodic signal into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or, equivalently, complex exponentials).
Figures for understanding Fourier Series.



Function s(x) (in red) is a sum of six sine functions of different amplitudes and harmonically related frequencies. Their summation is called a Fourier series. The Fourier transform, S(f) (in blue), which depicts amplitude vs frequency, reveals the 6 frequencies and their amplitudes.
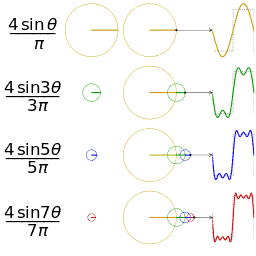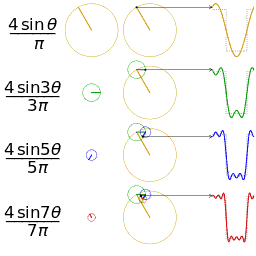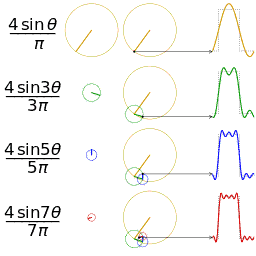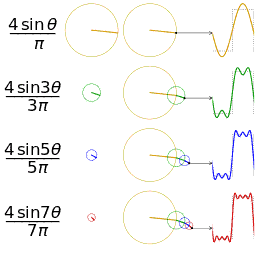
Another visualisation of an approximation of a square wave by taking the first 1, 2, 3 and 4 terms of its Fourier series
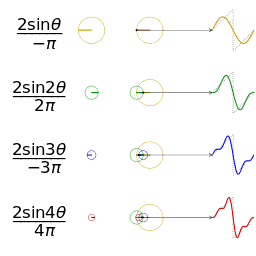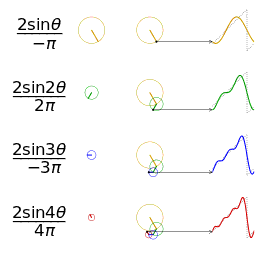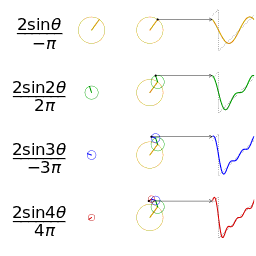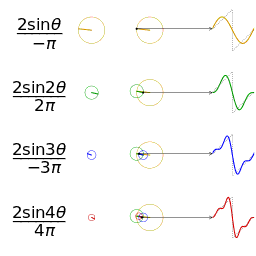
A visualisation of an approximation of a sawtooth wave of the same amplitude and frequency for comparison
Ref. (or copied from)
[1] http://en.wikipedia.org/wiki/Fourier_series
[2] http://physica.gsnu.ac.kr/phtml/wave/superpose/compositionfourier/compositionfourier4.html
[3] http://ko.wikipedia.org/wiki/%EB%94%94%EC%A7%80%ED%84%B8_%EC%8B%A0%ED%98%B8_%EC%B2%98%EB%A6%AC
[4] http://en.wikipedia.org/wiki/Digital_signal_processing
'Research > Mathmatics' 카테고리의 다른 글
| Skew symmetric matrix (0) | 2015.04.15 |
|---|---|
| Eigen Vectors and Eigen Values (0) | 2015.02.27 |
| What is homogeneous transform? (0) | 2015.01.16 |
| Atan2 에 대하여.. (what is atan2?) (0) | 2015.01.08 |
글
스페인 저가항공 부엘링(Vueling) 예약하기 (마드리드에서 바르셀로나)
Sky scanner를 활용해서 저렴하게 예약할 수 있는 항공편을 검색한다!!
(개인적으로 sky scanner는 이번 여행에 매우 유용한 사이트였다. http://www.skyscanner.co.kr/)
원하는 검색 조건으로 입력을 하니, 부엘링 항공이 가장 저렴한 것으로 검색 되었다!
자 이제, 부엘링 항공을 예약해 보자.
표를 구매하겠다고 하면 부엘링 항공의 홈페이지로 연결된다.
(이 가격대의 표가 어느 경로를 통해서 예약할 수 있는 지에 대한 정보가 함께 나온다.)
(나의 경우에는 부엘링 홈페이지에서 직접 하는 것이었음)
검색되었던 가격으로 잘 선택해서 예약을 해야 한다.
(비싼 가격 옵션도 있으니 조심하기를!)
다음 순서는 탑승자 정보를 입력하는 순서다!
탑승자 정보를 입력하고 나면, 좌석에 대한 옵션을 추가적으로 선택할 수 있다.
(옵션에 따라 추가 비용이 발생할 수 있으니 잘 확인하고 하도록 하자!)
마지막 순서는 결제 방법에 관한 것이다!
친절하게 설명이 되어 있으므로 편한 방식을 통해서 결제하면 된다.
(보통은 비자카드나 마스터카드를 사용할 것으로 예상된다)











