검색결과 리스트
Research/Mathmatics에 해당되는 글 5건
- 2015.04.15 Skew symmetric matrix
- 2015.02.27 Eigen Vectors and Eigen Values
- 2015.01.16 What is homogeneous transform?
- 2015.01.08 Atan2 에 대하여.. (what is atan2?)
- 2014.12.02 Fourier Transform (푸리에 변환)
글
Skew symmetric matrix
* ref
[1] https://moocs.qut.edu.au/courses/814/learn
'Research > Mathmatics' 카테고리의 다른 글
| Eigen Vectors and Eigen Values (0) | 2015.02.27 |
|---|---|
| What is homogeneous transform? (0) | 2015.01.16 |
| Atan2 에 대하여.. (what is atan2?) (0) | 2015.01.08 |
| Fourier Transform (푸리에 변환) (0) | 2014.12.02 |
글
Eigen Vectors and Eigen Values
아래 사이트의 동영상을 보면 정말 좋다.
https://www.khanacademy.org/math/linear-algebra/alternate_bases/eigen_everything/v/linear-algebra-finding-eigenvectors-and-eigenspaces-example
'Research > Mathmatics' 카테고리의 다른 글
| Skew symmetric matrix (0) | 2015.04.15 |
|---|---|
| What is homogeneous transform? (0) | 2015.01.16 |
| Atan2 에 대하여.. (what is atan2?) (0) | 2015.01.08 |
| Fourier Transform (푸리에 변환) (0) | 2014.12.02 |
글
What is homogeneous transform?
우선 homogeneous coordinate이 무엇인 지 생각해보자.
일례로, homogeneous coordinate에서는 (x, y)라는 하나의 포인트를 (x, y, 1)이라는 포인트로 표현한다.
이것은 projective plane 상의 점으로 생각하는 것이다. 조금 더 일반적으로 표현하자면 (wx, wy, w)로 표현할 수 있다. (하나의 표현으로 딱 정해진 것은 아님)
아래 페이지들을 보면 정말 설명이 잘 되어있기 때문에 나중에 다시 정리하도록 하자..
* Ref
http://blog.daum.net/shksjy/229
http://darkpgmr.tistory.com/78
Pose is described by just 3 numbers:
- Offset in the x-direction
- Offset in the y-direction
- A rotation angle
The homogeneous transformation is inefficient in this respect, requiring three times as many numbers as actually required. Some of those 9 numbers have fixed values like 0 or 1, and others repeated or repeated with a different sign. Its advantage is the ability to compound poses by matrix-matrix multiplication, or transform vectors by matrix-vector multiplication. These operations are very convenient to express in an environment like MATLAB, and with modern computers the extra computation required is almost insignificant.
In homogeneous coordinates a point and a line, on a plane, can both be represented by a 3-element vector.
An advantage of using the homogenous form is that it’s very easy to represent a line that is vertical where in Cartesian coordinates, that means that the grading of the line is equal to infinity. In homogeneous form, we treat that situation very simply and conveniently. We don’t need to introduce any infinities.
We also might be interested in how to describe a line that joins two points. So here we have two points and here’s a line that passes through those two points. Then the homogenous representation of the line which remember is the three vector is given simply by the cross-product of the two points that lie on the line. So a very, very simple way of finding the equation of a line that joins two points much, much more conveniently than it is for Cartesian coordinates.
* Ref :
[1] https://moocs.qut.edu.au/courses/814/learn
[2] https://moocs.qut.edu.au/courses/791/learn
'Research > Mathmatics' 카테고리의 다른 글
| Skew symmetric matrix (0) | 2015.04.15 |
|---|---|
| Eigen Vectors and Eigen Values (0) | 2015.02.27 |
| Atan2 에 대하여.. (what is atan2?) (0) | 2015.01.08 |
| Fourier Transform (푸리에 변환) (0) | 2014.12.02 |
글
Atan2 에 대하여.. (what is atan2?)
아래 내용은 끄적이는 것들이기 때문에 지속적으로 수정될 수 있음..
연구를 하다보면 삼각함수를 사용하게 될 경우가 많다.
특히 기구학 등을 analytic하게 풀기 위해서는 반드시 필요한 문제가 되겠다.
이 때 sin, cos 과 함께 자주 사용되는 녀석은 atan 함수라고 할 수 잇다.
이 문제는 일례로 HTransform matrix를 통해 roll, pitch, yaw로 표현되는 orientation을 구할 때 발생할 수 있다.
생각해보자. tangent함수는 pi를 주기로 반복되는 함수다. (그림은 구글에서 퍼왔음)

따라서 2pi 범위 내에서는 해가 두 가지 존재할 수 있겠다!
이것을 구분해 주는 방법이 필요하다는 사실을 직감할 수 있다!
(그렇지 않으면 아래와 같은 문제가 발생하겠지..)
그리고 또 한가지, tan함수는 불연속적으로 반복된다! pi/2 마다 infinite로 발산하고 있는 것을 알 수 있다.
이로 인해 우리가 고려해야 할 부분이 있다.atan의 인자로 사용되는 sin과 cos의 조합으로는 충분히 발생할 수 있는 문제가 있다는 것!
바로 분모가 0 이 되어 무한대가 발생하는 것!!
하지만 수학적으로 분모가 0이 된다는 것은 말이 되지 않는다.
그래서 우리는 알고리즘적으로 분모가 0에 매우 가까울 경우에는 atan의 값이 ' +-(2n-1)pi/2 , n은 정수 '라고 가정할 수 있겠다!
그래서 atan을 정상적으로 사용하기 위해서는 아래와 같은 가정이 필요하게 된다.
하지만 이 모든 알고리즘을 내포하고 있는 것이 바로 atan2가 되시겠다. 짜잔!! 대단하다.
다만 dx와 dy가 모두 0일 때에는 값이 정의되지 않음에 유의하자!
아래의 설명을 첨부한다. 굉장히 잘 설명하고 있다.
'Research > Mathmatics' 카테고리의 다른 글
| Skew symmetric matrix (0) | 2015.04.15 |
|---|---|
| Eigen Vectors and Eigen Values (0) | 2015.02.27 |
| What is homogeneous transform? (0) | 2015.01.16 |
| Fourier Transform (푸리에 변환) (0) | 2014.12.02 |
글
Fourier Transform (푸리에 변환)
한 지점에서의 파동의 움직임을 계속 관측하면 주어진 각각의 시간에 파동량의 그래프를 그릴 수 있을 것이다. 이 그래프는 모든 시간 값에 대하여 대응되는 파동량을 가지고 있는 아날로그의 데이터일 것인데 이 신호를 컴퓨터를 통해서 읽으면 띄엄띄엄한 시간에 띄엄띄엄한 파동량의 디지털화 된 데이터로 될 것이다.
예를 들어 소리의 전기신호를 오실로스코프로 보면 음압이나 변위에 대한 연속적인 그래프가 화면에 바로 나타날 것이다. 이 신호를 푸리에 해석을 하여 주파수 성분을 추출하고자 한다면 앞에서 설명한 대로 여러번 적분을 행해야 할 것이다. 그러나 음압을 나타내는 전기신호는 보통 해석적인 함수가 아니므로 해석적으로 적분을 할 수 없게 되어 수치해석이 필요해 진다. 콘덴서나 코일 등의 소자를 구성해서 아날로그로의 푸리에 해석을 어느 정도는 해 낼 수 있지만 엄밀한 분석은 불가능하다.
컴퓨터를 이용한 신호분석
음파의 신호를 컴퓨터를 통해서 읽게 되면 수치해석을 컴퓨터의 연산능력으로 푸리에 해석을 할 수 있게 된다. 이 경우 컴퓨터는 신호의 변화에 대하여는 매우 짧은 시간간격이긴 하지만 어떤 유한한 간격으로 신호를 읽을 수밖에 없을 것이다. 측정의 시간 간격을 줄이면 줄일수록 원래의 아날로그 데이터에 근접하게 되겠지만 같은 시간분량에 대한 데이터 수는 시간간격에 반비례하여 늘어가게 되어 컴퓨터가 감당하지 못하게 된다. 한편 어떤 시간의 측정 값도 당연히 디지털화 된 신호일 수밖에 없다. 따라서 연속적인 모든 값을 표현하지 못하고 불연속적인 값들 중 하나로 나타내어지게 된다. 시간 축으로나 신호 축으로나 이렇게 띄엄띄엄하게 측정되는 것을 양자화되었다고 한다.
| graph |
 |
|
음악을 기록한 것 중 옛날의 LP 판은 음파의 변화를 연속적으로 기록해 둔, 일종의 아날로그형의 신호 기록으로 볼 수 있고, CD나 DAT 등은 음파를 디지털화 시켜 기록한 것으로 비교해 볼 수 있다. CD의 경우 1초에 4만번 이상으로 한 번에 16비트, 즉 6만 계단 이상으로 음을 기록해서 이를 재생하면 아날로그의 원형을 거의 완벽하게 재생해 낼 수 있게 된다. 아날로그 기록인 경우 신호가 정확하게 읽혀지지 않을 가능성이 있지만 값으로 기록된 디지털 기록은 언제나 정확하게 읽혀지게 되고 통신을 통해서도 정확하게 전달 시킬 수 있게 된다.
디지털화된 신호는 { 1.1, 1.2, 1.34, ... } 처럼 일종의 수열로서 시간 순서로 이루어져 있다면 시계열(time series)라고 한다. 이 데이터를 이제 컴퓨터에서 수치해석으로 적분하여 그 신호가 가지고 있는 각각의 주파수 성분, 즉 스펙트럼을 계산해 낼 수 있게 된다. 이에 관련된 기법을 DFT(discrete fourier transformation)라 하여 디지털 신호처리(DSP: digital signal processing) 기술의 핵심을 이루게 된다. 즉 음성인식이나 변조, 복원 등 여러 가지 기법이 DSP를 통해서 가능하게 되었다.
* 디지털 신호 처리
디지털 신호 처리(Digital signal processing, DSP)는 디지털화된 신호를 원하는 방향으로 정보 신호를 수정하거나 개선할 목적으로 알고리즘에 의해 수치적으로 처리하는 것을 말한다. 보통 아날로그 신호를 디지털화하는 과정에서 이산 신호가 되고 수치화 된다.
DSP의 일반적인 목적은 연속적인 실세계 아날로그 신호를 측정하고 걸러내고 압축하는 것이다. 첫 단계는 샘플링이라는 과정을 통해 신호를 아날로그에서 디지털 형태로 변환하는 것이고, 그 뒤 ADC를 이용하여 디지털화하여 아날로그 신호를 연속된 수로 바꾼다.
The goal of DSP is usually to measure, filter and/or compress continuous real-world analog signals. Usually, the first step is conversion of the signal from an analog to a digital form, by sampling and then digitizing it using an analog-to-digital converter (ADC), which turns the analog signal into a stream of discrete digital values. Often, however, the required output signal is also analog, which requires a digital-to-analog converter (DAC). Even if this process is more complex than analog processing and has a discrete value range, the application of computational power to signal processing allows for many advantages over analog processing in many applications, such as error detection and correction in transmission as well as data compression.[1]
FFT 해석
매우 빠르게 푸리에 분석을 수행한다.
분석해야 할 시계열의 데이터가
한편 데이터가
* Fourier Analysis
- Continuous-Time Fourier Series
- Continuous-Time Fourier Transform
- Discrete-Time Fourier Series
- Discrete-Time Fourier Transform
* Fourier Series
- A way to represent a wave-like function as the sum of simple sine waves.
More formally, it decomposes any periodic function or periodic signal into the sum of a (possibly infinite) set of simple oscillating functions, namely sines and cosines (or, equivalently, complex exponentials).
Figures for understanding Fourier Series.



Function s(x) (in red) is a sum of six sine functions of different amplitudes and harmonically related frequencies. Their summation is called a Fourier series. The Fourier transform, S(f) (in blue), which depicts amplitude vs frequency, reveals the 6 frequencies and their amplitudes.
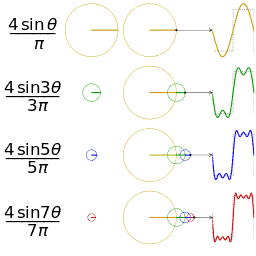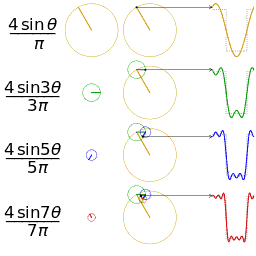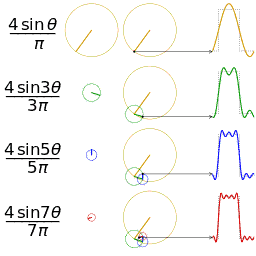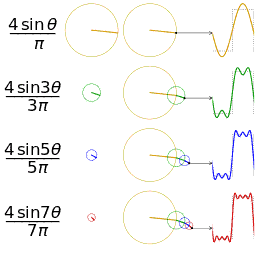
Another visualisation of an approximation of a square wave by taking the first 1, 2, 3 and 4 terms of its Fourier series
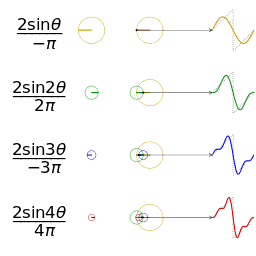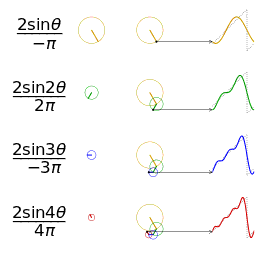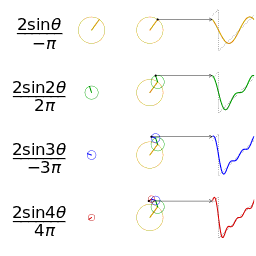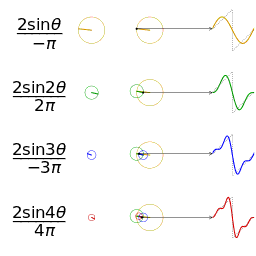
A visualisation of an approximation of a sawtooth wave of the same amplitude and frequency for comparison
Ref. (or copied from)
[1] http://en.wikipedia.org/wiki/Fourier_series
[2] http://physica.gsnu.ac.kr/phtml/wave/superpose/compositionfourier/compositionfourier4.html
[3] http://ko.wikipedia.org/wiki/%EB%94%94%EC%A7%80%ED%84%B8_%EC%8B%A0%ED%98%B8_%EC%B2%98%EB%A6%AC
[4] http://en.wikipedia.org/wiki/Digital_signal_processing
'Research > Mathmatics' 카테고리의 다른 글
| Skew symmetric matrix (0) | 2015.04.15 |
|---|---|
| Eigen Vectors and Eigen Values (0) | 2015.02.27 |
| What is homogeneous transform? (0) | 2015.01.16 |
| Atan2 에 대하여.. (what is atan2?) (0) | 2015.01.08 |










